Distributions - R#

Normal Distribution#

Parameterization: mean (μ): mean, standard deviation (σ): sd
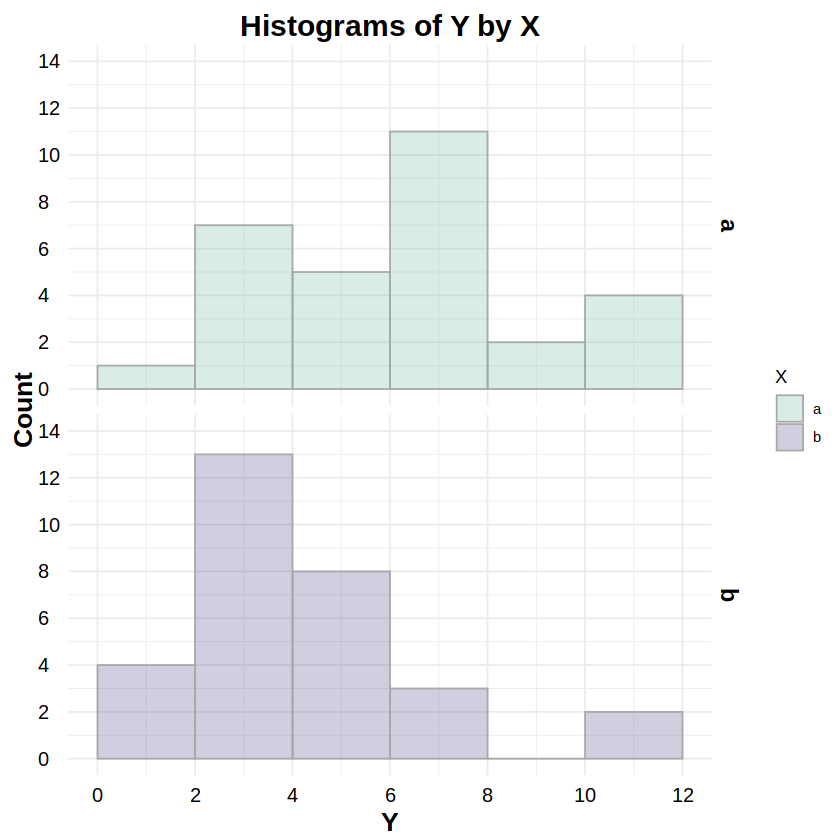
Distribution Functions: _norm: dnorm, pnorm, qnorm, rnorm
Reporting: “Figure 2 shows the distributions of response Y for both levels of factor X. To test whether these distributions were normally distributed, a Kolmogorov-Smirnov test was run on Y for both levels of X. The test for level ‘a’ was statistically non-significant (D = .158, p = .404), as was the test for level ‘b’ (D = .104, p = .867), indicating non-detectable deviations from a normal distribution for both levels.”

# Example data
# df has one factor (X) w/two levels (a,b) and continuous response Y
df <- read.csv("data/1F2LBs_normal.csv")
head(df, 20)

A data.frame: 20 × 3
	S	X	Y
	<int>	<chr>	<dbl>
1	1	a	10.055297
2	2	b	11.462669
3	3	a	12.140244
4	4	b	14.025322
5	5	a	6.922079
6	6	b	16.523659
7	7	a	7.350582
8	8	b	13.416170
9	9	a	11.279275
10	10	b	12.571377
11	11	a	12.216500
12	12	b	12.017293
13	13	a	10.485682
14	14	b	14.422881
15	15	a	12.127070
16	16	b	16.750440
17	17	a	8.874990
18	18	b	11.498568
19	19	a	11.509413
20	20	b	13.603714

library(MASS) # for fitdistr
fa = fitdistr(df[df$X == "a",]$Y, "normal")$estimate # create fit for X.a
ks.test(df[df$X == "a",]$Y, "pnorm", mean=fa[1], sd=fa[2])
fb = fitdistr(df[df$X == "b",]$Y, "normal")$estimate # create fit for X.b
ks.test(df[df$X == "b",]$Y, "pnorm", mean=fb[1], sd=fb[2])

	Exact one-sample Kolmogorov-Smirnov test

data:  df[df$X == "a", ]$Y
D = 0.15752, p-value = 0.4042
alternative hypothesis: two-sided

	Exact one-sample Kolmogorov-Smirnov test

data:  df[df$X == "b", ]$Y
D = 0.10418, p-value = 0.8674
alternative hypothesis: two-sided

library(ggplot2)
library(ggthemes)
library(scales)

# Histograms
# http://www.sthda.com/english/wiki/ggplot2-histogram-plot-quick-start-guide-r-software-and-data-visualization
ggplot(data=df, aes(x=Y, col=X, fill=X)) + theme_minimal() + 
  # set the font styles for the plot title and axis titles
  theme(plot.title   = element_text(face="bold",  color="black", size=18, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.title.x = element_text(face="bold",  color="black", size=16, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.title.y = element_text(face="bold",  color="black", size=16, hjust=0.5, vjust=0.0, angle=90)) + 
  # set the font styles for the value labels that show on each axis
  theme(axis.text.x  = element_text(face="plain", color="black", size=12, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.text.y  = element_text(face="plain", color="black", size=12, hjust=0.0, vjust=0.5, angle=0)) + 
  # set the font style for the facet labels
  theme(strip.text = element_text(face="bold", color="black", size=14, hjust=0.5)) + 
  # create the histogram; the alpha value ensures overlaps can be seen
  geom_histogram(color="darkgray", binwidth=1, breaks=seq(4,18,by=1), alpha=0.25, position="identity") + 
  # create stacked plots by X, one for each histogram
  facet_grid(X ~ .) + 
  # determine the fill color values of each histogram
  scale_fill_manual(values=c("#69b3a2","#404080")) + 
  # set the labels for the title and each axis
  labs(title="Histograms of Y by X", x="Y", y="Count") + 
  # set the ranges and value labels for each axis
  scale_x_continuous(breaks=seq(4,18,by=1), labels=seq(4,18,by=1), limits=c(4,18)) +
  scale_y_continuous(breaks=seq(0,8,by=2), labels=seq(0,8,by=2), limits=c(0,8))

Lognormal Distribution#

Parameterization: mean (μ): meanlog, standard deviation (σ): sdlog
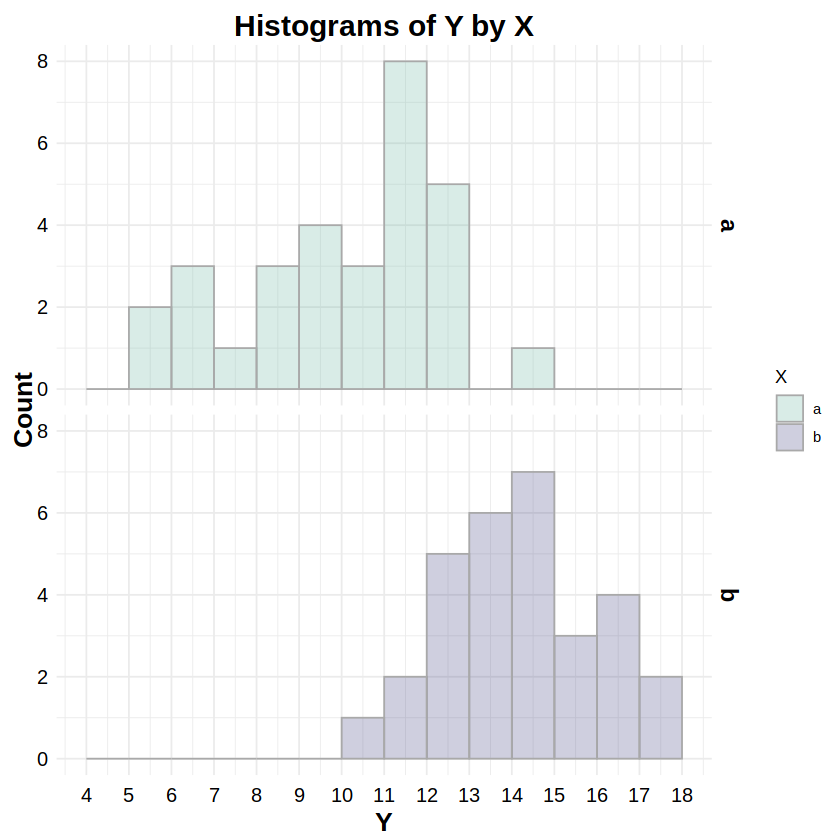
Distribution Functions: _lnorm: dlnorm, plnorm, qlnorm, rlnorm
Reporting: “Figure 3 shows the distributions of response Y for both levels of factor X. To test whether these distributions were lognormally distributed, a Kolmogorov-Smirnov test was run on Y for both levels of X. The test for level ‘a’ was statistically non-significant (D = .096, p = .918), as was the test for level ‘b’ (D = .161, p = .375), indicating non-detectable deviations from a lognormal distribution for both levels.”

# Example data
# df has one factor (X) w/two levels (a,b) and continuous response Y
df <- read.csv("data/1F2LBs_lognormal.csv")
head(df, 20)

A data.frame: 20 × 3
	S	X	Y
	<int>	<chr>	<dbl>
1	1	a	18.308269
2	2	b	5.951342
3	3	a	5.739954
4	4	b	5.932270
5	5	a	21.378222
6	6	b	25.155509
7	7	a	20.848274
8	8	b	6.533354
9	9	a	8.683973
10	10	b	11.213393
11	11	a	6.517906
12	12	b	19.214861
13	13	a	1.084347
14	14	b	11.620167
15	15	a	1.334683
16	16	b	12.304836
17	17	a	14.400186
18	18	b	18.914468
19	19	a	3.369996
20	20	b	5.535679

library(MASS) # for fitdistr
fa = fitdistr(df[df$X == "a",]$Y, "lognormal")$estimate # create fit for X.a
ks.test(df[df$X == "a",]$Y, "plnorm", meanlog=fa[1], sdlog=fa[2])
fb = fitdistr(df[df$X == "b",]$Y, "lognormal")$estimate # create fit for X.b
ks.test(df[df$X == "b",]$Y, "plnorm", meanlog=fb[1], sdlog=fb[2])

	Exact one-sample Kolmogorov-Smirnov test

data:  df[df$X == "a", ]$Y
D = 0.0964, p-value = 0.918
alternative hypothesis: two-sided

	Exact one-sample Kolmogorov-Smirnov test

data:  df[df$X == "b", ]$Y
D = 0.16135, p-value = 0.3752
alternative hypothesis: two-sided

library(ggplot2)
library(ggthemes)
library(scales)

# Plot lognormal histograms
# http://www.sthda.com/english/wiki/ggplot2-histogram-plot-quick-start-guide-r-software-and-data-visualization
ggplot(data=df, aes(x=Y, col=X, fill=X)) + theme_minimal() + 
  # set the font styles for the plot title and axis titles
  theme(plot.title   = element_text(face="bold",  color="black", size=18, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.title.x = element_text(face="bold",  color="black", size=16, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.title.y = element_text(face="bold",  color="black", size=16, hjust=0.5, vjust=0.0, angle=90)) + 
  # set the font styles for the value labels that show on each axis
  theme(axis.text.x  = element_text(face="plain", color="black", size=12, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.text.y  = element_text(face="plain", color="black", size=12, hjust=0.0, vjust=0.5, angle=0)) + 
  # set the font style for the facet labels
  theme(strip.text = element_text(face="bold", color="black", size=14, hjust=0.5)) + 
  # create the histogram; the alpha value ensures overlaps can be seen
  geom_histogram(color="darkgray", binwidth=10, breaks=seq(0,80,by=10), alpha=0.25, position="identity") + 
  # create stacked plots by X, one for each histogram
  facet_grid(X ~ .) + 
  # determine the fill color values of each histogram
  scale_fill_manual(values=c("#69b3a2","#404080")) + 
  # set the labels for the title and each axis
  labs(title="Histograms of Y by X", x="Y", y="Count") + 
  # set the ranges and value labels for each axis
  scale_x_continuous(breaks=seq(0,80,by=10), labels=seq(0,80,by=10), limits=c(0,80)) +
  scale_y_continuous(breaks=seq(0,20,by=4), labels=seq(0,20,by=4), limits=c(0,20))

Poisson Distribution#

Parameterization: lambda (λ): lambda
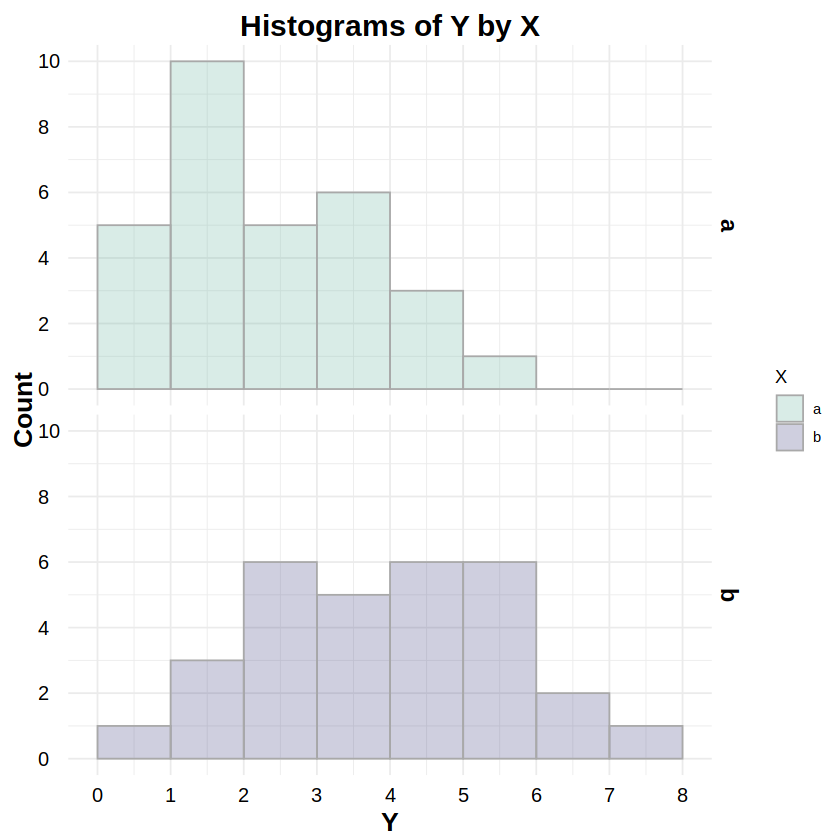
Distribution Functions: _pois: dpois, ppois, qpois, rpois
Reporting: “Figure 4 shows the distributions of response Y for both levels of factor X. To test whether these distributionswere Poisson distributed, a Chi-Squared goodness-of-fit test was run on Y for both levels of X. The test for level ‘a’ was statistically non-significant (χ2(3, N=30) = 2.62, p = .454), as was the test for level ‘b’ (χ2(4, N=30) = 2.79, p = .593), indicating non-detectable deviations from a Poisson distribution for both levels.”

# Example data
# df has one factor (X) w/two levels (a,b) and nonnegative integer response Y
df <- read.csv("data/1F2LBs_poisson.csv")
head(df, 20)

A data.frame: 20 × 3
	S	X	Y
	<int>	<chr>	<int>
1	1	a	5
2	2	b	6
3	3	a	3
4	4	b	3
5	5	a	3
6	6	b	5
7	7	a	5
8	8	b	7
9	9	a	2
10	10	b	4
11	11	a	2
12	12	b	5
13	13	a	0
14	14	b	5
15	15	a	0
16	16	b	6
17	17	a	2
18	18	b	3
19	19	a	4
20	20	b	6

library(fitdistrplus) # for fitdist, gofstat
fa = fitdist(df[df$X == "a",]$Y, "pois") # create fit for X.a
gofstat(fa)
fb = fitdist(df[df$X == "b",]$Y, "pois") # create fit for X.b
gofstat(fb)

Loading required package: survival

Chi-squared statistic:  2.619401 
Degree of freedom of the Chi-squared distribution:  3 
Chi-squared p-value:  0.4540985 
   the p-value may be wrong with some theoretical counts < 5  
Chi-squared table:
     obscounts theocounts
<= 1  5.000000   7.280252
<= 2 10.000000   7.284586
<= 3  5.000000   6.637067
<= 4  6.000000   4.535329
> 4   4.000000   4.262765

Goodness-of-fit criteria
                               1-mle-pois
Akaike's Information Criterion   112.8951
Bayesian Information Criterion   114.2962

Chi-squared statistic:  2.794443 
Degree of freedom of the Chi-squared distribution:  4 
Chi-squared p-value:  0.5927924 
   the p-value may be wrong with some theoretical counts < 5  
Chi-squared table:
     obscounts theocounts
<= 2  4.000000   5.436500
<= 3  6.000000   5.173554
<= 4  5.000000   5.734022
<= 5  6.000000   5.084166
<= 6  6.000000   3.756634
> 6   3.000000   4.815124

Goodness-of-fit criteria
                               1-mle-pois
Akaike's Information Criterion   121.0369
Bayesian Information Criterion   122.4381

library(ggplot2)
library(ggthemes)
library(scales)

# Plot Poisson histograms
# http://www.sthda.com/english/wiki/ggplot2-histogram-plot-quick-start-guide-r-software-and-data-visualization
ggplot(data=df, aes(x=Y, col=X, fill=X)) + theme_minimal() + 
  # set the font styles for the plot title and axis titles
  theme(plot.title   = element_text(face="bold",  color="black", size=18, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.title.x = element_text(face="bold",  color="black", size=16, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.title.y = element_text(face="bold",  color="black", size=16, hjust=0.5, vjust=0.0, angle=90)) + 
  # set the font styles for the value labels that show on each axis
  theme(axis.text.x  = element_text(face="plain", color="black", size=12, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.text.y  = element_text(face="plain", color="black", size=12, hjust=0.0, vjust=0.5, angle=0)) + 
  # set the font style for the facet labels
  theme(strip.text = element_text(face="bold", color="black", size=14, hjust=0.5)) + 
  # create the histogram; the alpha value ensures overlaps can be seen
  geom_histogram(color="darkgray", binwidth=1, breaks=seq(0,8,by=1), alpha=0.25, position="identity") + 
  # create stacked plots by X, one for each histogram
  facet_grid(X ~ .) + 
  # determine the fill color values of each histogram
  scale_fill_manual(values=c("#69b3a2","#404080")) + 
  # set the labels for the title and each axis
  labs(title="Histograms of Y by X", x="Y", y="Count") + 
  # set the ranges and value labels for each axis
  scale_x_continuous(breaks=seq(0,8,by=1), labels=seq(0,8,by=1), limits=c(0,8)) +
  scale_y_continuous(breaks=seq(0,10,by=2), labels=seq(0,10,by=2), limits=c(0,10))

Negative Binomial Distribution#

Parameterization: theta (θ): theta, mu (μ): mu
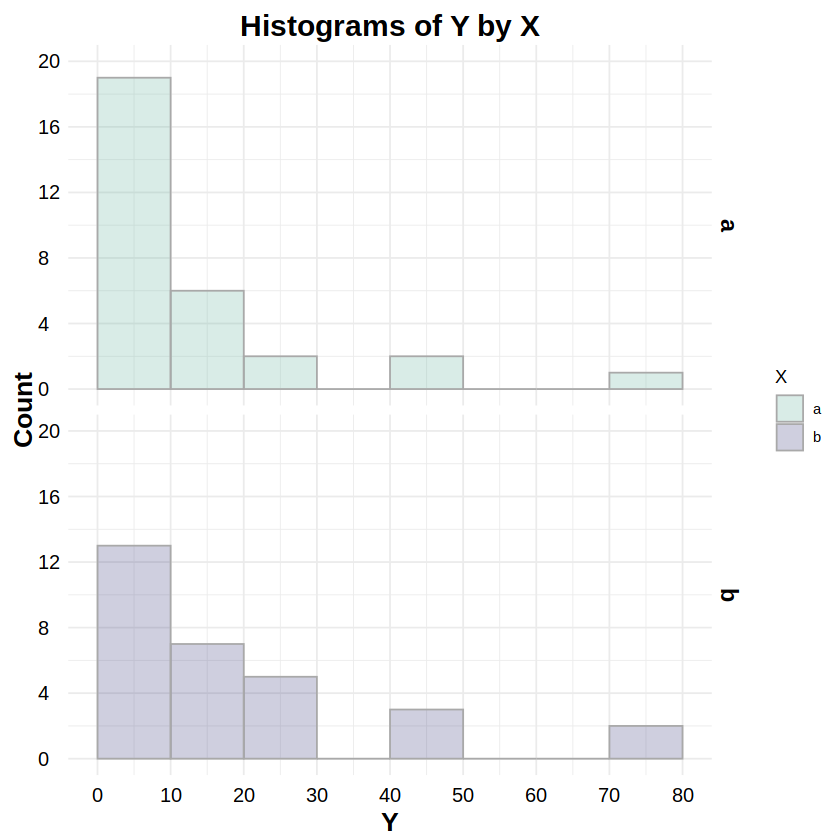
Distribution Functions: _nbinom: dnbinom, pnbinom, qnbinom, rnbinom
Reporting: “Figure 5 shows the distributions of response Y for both levels of factor X. To test whether these distributions were negative binomially distributed, a Chi-Squared goodness-of-fit test was run on Y for both levels of X. The test for level ‘a’ was statistically non-significant (χ2(4, N=30) = 1.74, p = .783), as was the test for level ‘b’ (χ2(3, N=30) = 1.27, p = .737), indicating non-detectable deviations from a negative binomial distribution for both levels.”

# Example data
# df has one factor (X) w/two levels (a,b) and nonnegative integer response Y
df <- read.csv("data/1F2LBs_negbin.csv")
head(df, 20)

A data.frame: 20 × 3
	S	X	Y
	<int>	<chr>	<int>
1	1	a	22
2	2	b	11
3	3	a	16
4	4	b	9
5	5	a	8
6	6	b	16
7	7	a	13
8	8	b	4
9	9	a	18
10	10	b	10
11	11	a	15
12	12	b	6
13	13	a	27
14	14	b	19
15	15	a	15
16	16	b	14
17	17	a	22
18	18	b	20
19	19	a	36
20	20	b	10

library(fitdistrplus) # for fitdist, gofstat
fa = fitdist(df[df$X == "a",]$Y, "nbinom") # create fit for X.a
gofstat(fa)
fb = fitdist(df[df$X == "b",]$Y, "nbinom") # create fit for X.b
gofstat(fb)

Chi-squared statistic:  1.73975 
Degree of freedom of the Chi-squared distribution:  4 
Chi-squared p-value:  0.7834849 
   the p-value may be wrong with some theoretical counts < 5  
Chi-squared table:
      obscounts theocounts
<= 7   5.000000   3.498637
<= 11  4.000000   5.021527
<= 14  5.000000   4.274380
<= 18  4.000000   5.293625
<= 23  4.000000   5.056978
<= 28  4.000000   3.214631
> 28   4.000000   3.640223

Goodness-of-fit criteria
                               1-mle-nbinom
Akaike's Information Criterion     217.6756
Bayesian Information Criterion     220.4780

Chi-squared statistic:  1.268287 
Degree of freedom of the Chi-squared distribution:  3 
Chi-squared p-value:  0.736677 
   the p-value may be wrong with some theoretical counts < 5  
Chi-squared table:
      obscounts theocounts
<= 5   4.000000   3.954289
<= 8   6.000000   5.716970
<= 10  4.000000   4.235641
<= 13  4.000000   5.710654
<= 16  6.000000   4.245423
> 16   6.000000   6.137024

Goodness-of-fit criteria
                               1-mle-nbinom
Akaike's Information Criterion     194.1103
Bayesian Information Criterion     196.9126

library(ggplot2)
library(ggthemes)
library(scales)

# Plot negative binomial histograms
# http://www.sthda.com/english/wiki/ggplot2-histogram-plot-quick-start-guide-r-software-and-data-visualization
ggplot(data=df, aes(x=Y, col=X, fill=X)) + theme_minimal() + 
  # set the font styles for the plot title and axis titles
  theme(plot.title   = element_text(face="bold",  color="black", size=18, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.title.x = element_text(face="bold",  color="black", size=16, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.title.y = element_text(face="bold",  color="black", size=16, hjust=0.5, vjust=0.0, angle=90)) + 
  # set the font styles for the value labels that show on each axis
  theme(axis.text.x  = element_text(face="plain", color="black", size=12, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.text.y  = element_text(face="plain", color="black", size=12, hjust=0.0, vjust=0.5, angle=0)) + 
  # set the font style for the facet labels
  theme(strip.text = element_text(face="bold", color="black", size=14, hjust=0.5)) + 
  # create the histogram; the alpha value ensures overlaps can be seen
  geom_histogram(color="darkgray", binwidth=5, breaks=seq(0,40,by=5), alpha=0.25, position="identity") + 
  # create stacked plots by X, one for each histogram
  facet_grid(X ~ .) + 
  # determine the fill color values of each histogram
  scale_fill_manual(values=c("#69b3a2","#404080")) + 
  # set the labels for the title and each axis
  labs(title="Histograms of Y by X", x="Y", y="Count") + 
  # set the ranges and value labels for each axis
  scale_x_continuous(breaks=seq(0,40,by=5), labels=seq(0,40,by=5), limits=c(0,40)) +
  scale_y_continuous(breaks=seq(0,10,by=2), labels=seq(0,10,by=2), limits=c(0,10))

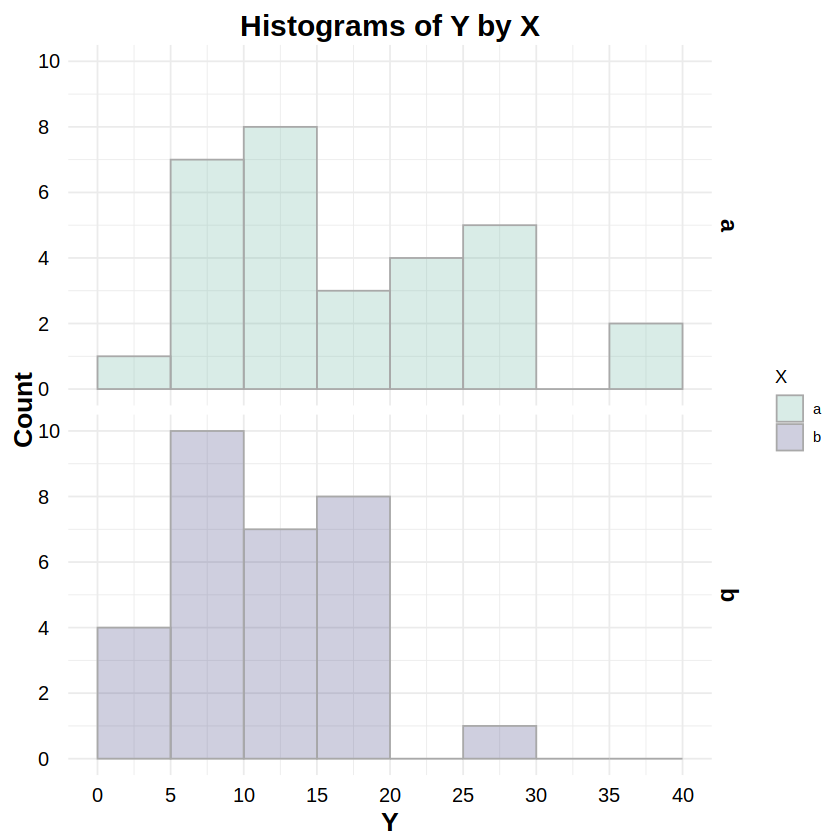
Exponential Distribution#

Parameterization: rate (λ): rate
Distribution Functions: _exp: dexp, pexp, qexp, rexp
Reporting: “Figure 6 shows the distributions of response Y for both levels of factor X. To test whether these distributions were exponentially distributed, a Kolmogorov-Smirnov test was run on Y for both levels of X. The test for level ‘a’ was statistically non-significant (D = .107, p = .849), as was the test for level ‘b’ (D = .119, p = .742), indicating non-detectable deviations from an exponential distribution for both levels.”

# Example data
# df has one factor (X) w/two levels (a,b) and continuous response Y
df <- read.csv("data/1F2LBs_exponential.csv")
head(df, 20)

A data.frame: 20 × 3
	S	X	Y
	<int>	<chr>	<dbl>
1	1	a	12.477962
2	2	b	5.975198
3	3	a	7.781088
4	4	b	16.940324
5	5	a	10.526902
6	6	b	4.675437
7	7	a	9.899636
8	8	b	23.608037
9	9	a	2.041000
10	10	b	5.257079
11	11	a	43.238041
12	12	b	13.202714
13	13	a	8.352570
14	14	b	5.377658
15	15	a	16.142961
16	16	b	1.901692
17	17	a	1.372129
18	18	b	12.738519
19	19	a	2.903349
20	20	b	25.792198

library(MASS) # for fitdistr
fa = fitdistr(df[df$X == "a",]$Y, "exponential")$estimate # create fit for X.a
ks.test(df[df$X == "a",]$Y, "pexp", rate=fa[1])
fb = fitdistr(df[df$X == "b",]$Y, "exponential")$estimate # create fit for X.b
ks.test(df[df$X == "b",]$Y, "pexp", rate=fb[1])

	Exact one-sample Kolmogorov-Smirnov test

data:  df[df$X == "a", ]$Y
D = 0.10665, p-value = 0.8491
alternative hypothesis: two-sided

	Exact one-sample Kolmogorov-Smirnov test

data:  df[df$X == "b", ]$Y
D = 0.11942, p-value = 0.7415
alternative hypothesis: two-sided

library(ggplot2)
library(ggthemes)
library(scales)

# Plot exponential histograms
# http://www.sthda.com/english/wiki/ggplot2-histogram-plot-quick-start-guide-r-software-and-data-visualization
ggplot(data=df, aes(x=Y, col=X, fill=X)) + theme_minimal() + 
  # set the font styles for the plot title and axis titles
  theme(plot.title   = element_text(face="bold",  color="black", size=18, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.title.x = element_text(face="bold",  color="black", size=16, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.title.y = element_text(face="bold",  color="black", size=16, hjust=0.5, vjust=0.0, angle=90)) + 
  # set the font styles for the value labels that show on each axis
  theme(axis.text.x  = element_text(face="plain", color="black", size=12, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.text.y  = element_text(face="plain", color="black", size=12, hjust=0.0, vjust=0.5, angle=0)) + 
  # set the font style for the facet labels
  theme(strip.text = element_text(face="bold", color="black", size=14, hjust=0.5)) + 
  # create the histogram; the alpha value ensures overlaps can be seen
  geom_histogram(color="darkgray", binwidth=5, breaks=seq(0,50,by=5), alpha=0.25, position="identity") + 
  # create stacked plots by X, one for each histogram
  facet_grid(X ~ .) + 
  # determine the fill color values of each histogram
  scale_fill_manual(values=c("#69b3a2","#404080")) + 
  # set the labels for the title and each axis
  labs(title="Histograms of Y by X", x="Y", y="Count") + 
  # set the ranges and value labels for each axis
  scale_x_continuous(breaks=seq(0,50,by=5), labels=seq(0,50,by=5), limits=c(0,50)) +
  scale_y_continuous(breaks=seq(0,14,by=2), labels=seq(0,14,by=2), limits=c(0,14))

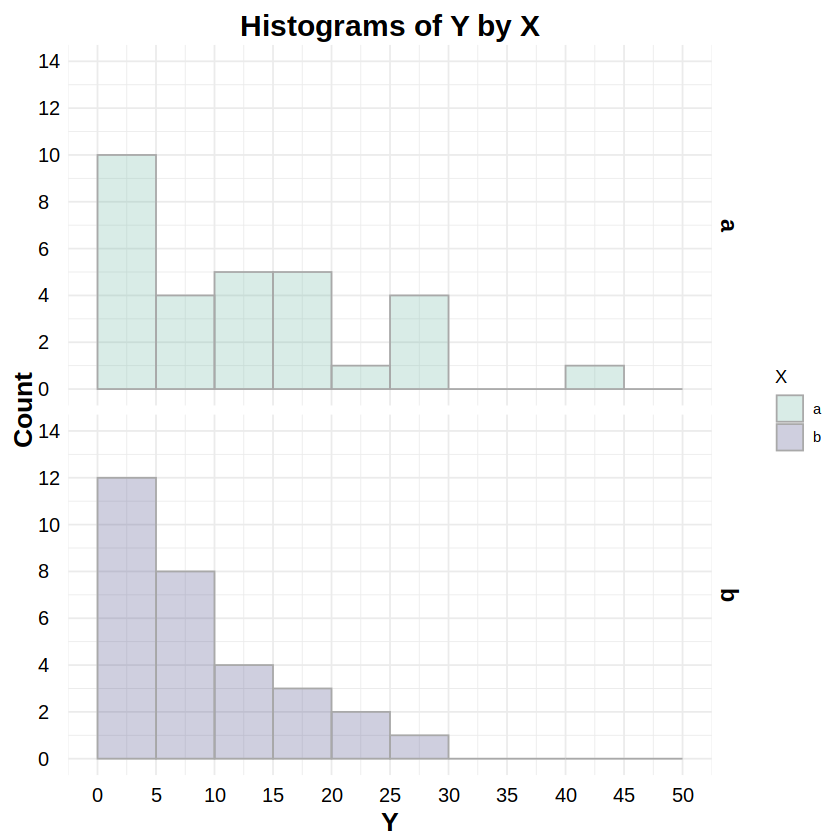
Gamma Distribution#

Parameterization: shape (α): shape, rate (β): rate
Distribution Functions: _gamma: dgamma, pgamma, qgamma, rgamma
Reporting: “Figure 7 shows the distributions of response Y for both levels of factor X. To test whether these distributions were Gamma distributed, a Kolmogorov-Smirnov test was run on Y for both levels of X. The test for level ‘a’ was statistically non-significant (D = .116, p = .773), as was the test for level ‘b’ (D = .143, p = .526), indicating non-detectable deviations from a Gamma distribution for both levels.”

# Example data
# df has one factor (X) w/two levels (a,b) and continuous response Y
df <- read.csv("data/1F2LBs_gamma.csv")
head(df, 20)

A data.frame: 20 × 3
	S	X	Y
	<int>	<chr>	<dbl>
1	1	a	10.345366
2	2	b	1.409266
3	3	a	6.433979
4	4	b	3.092545
5	5	a	3.943187
6	6	b	2.696895
7	7	a	4.507424
8	8	b	2.838128
9	9	a	5.451457
10	10	b	11.115251
11	11	a	5.308393
12	12	b	2.263850
13	13	a	6.573330
14	14	b	5.052664
15	15	a	3.564134
16	16	b	3.250415
17	17	a	10.281266
18	18	b	2.987387
19	19	a	3.656736
20	20	b	2.773202

library(MASS) # for fitdistr
fa = fitdistr(df[df$X == "a",]$Y, "gamma")$estimate # create fit for X.a
ks.test(df[df$X == "a",]$Y, "pgamma", shape=fa[1], rate=fa[2])
fb = fitdistr(df[df$X == "b",]$Y, "gamma")$estimate # create fit for X.b
ks.test(df[df$X == "b",]$Y, "pgamma", shape=fb[1], rate=fb[2])

	Exact one-sample Kolmogorov-Smirnov test

data:  df[df$X == "a", ]$Y
D = 0.11585, p-value = 0.7732
alternative hypothesis: two-sided

	Exact one-sample Kolmogorov-Smirnov test

data:  df[df$X == "b", ]$Y
D = 0.14293, p-value = 0.5258
alternative hypothesis: two-sided

library(ggplot2)
library(ggthemes)
library(scales)

# Plot gamma histograms
# http://www.sthda.com/english/wiki/ggplot2-histogram-plot-quick-start-guide-r-software-and-data-visualization
ggplot(data=df, aes(x=Y, col=X, fill=X)) + theme_minimal() + 
  # set the font styles for the plot title and axis titles
  theme(plot.title   = element_text(face="bold",  color="black", size=18, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.title.x = element_text(face="bold",  color="black", size=16, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.title.y = element_text(face="bold",  color="black", size=16, hjust=0.5, vjust=0.0, angle=90)) + 
  # set the font styles for the value labels that show on each axis
  theme(axis.text.x  = element_text(face="plain", color="black", size=12, hjust=0.5, vjust=0.0, angle=0)) + 
  theme(axis.text.y  = element_text(face="plain", color="black", size=12, hjust=0.0, vjust=0.5, angle=0)) + 
  # set the font style for the facet labels
  theme(strip.text = element_text(face="bold", color="black", size=14, hjust=0.5)) + 
  # create the histogram; the alpha value ensures overlaps can be seen
  geom_histogram(color="darkgray", binwidth=2, breaks=seq(0,12,by=2), alpha=0.25, position="identity") + 
  # create stacked plots by X, one for each histogram
  facet_grid(X ~ .) + 
  # determine the fill color values of each histogram
  scale_fill_manual(values=c("#69b3a2","#404080")) + 
  # set the labels for the title and each axis
  labs(title="Histograms of Y by X", x="Y", y="Count") + 
  # set the ranges and value labels for each axis
  scale_x_continuous(breaks=seq(0,12,by=2), labels=seq(0,12,by=2), limits=c(0,12)) +
  scale_y_continuous(breaks=seq(0,14,by=2), labels=seq(0,14,by=2), limits=c(0,14))

Statistical Analysis and Reporting

Distributions - R

Contents

Distributions - R#

Normal Distribution#

Lognormal Distribution#

Poisson Distribution#

Negative Binomial Distribution#

Exponential Distribution#

Gamma Distribution#